Biopharmaceutical Process Control: Part Two: Process Modeling
Development of a commercial product from a cell culture or a recombinant microbe can be greatly enhanced if the same control system configuration environment, control toolset, historian, HMI, and alarm and event database are used from the bench top through pilot scale to production.
Online process models deployed on a control system common to development and production offer many advantages.
They can:
- help control process and sensor non-linearities
- allow for creation and testing of control strategies and batch recipes before clinical material is required if a process is represented by a high fidelity model.
In process development, high fidelity modeling can be used to determine the impact of operating conditions on yield and product quality. In production, on-line multivariate statistical modeling can help detect abnormal conditions and predict quality parameters at the end of the batch.
Where Part 1 of this article focused on developments in sensors for bioprocess control, this article will examine bioprocess modeling options, focusing on three types of models, all of which can run on a distributed control system (DCS):
- First order plus dead time (FOPDT)
- High fidelity
- Multivariate statistics.
Insight into changes during batch operation may be gained through the identification of simple first order plus deadtime (FOPDT) models at different points in the batch. The article will also examine the structure of a high fidelity model, exploring its use in process development and plant design.
In addition, the article will examine how PLS (for Partial Least Squares, or, if you prefer,Projection to Latent Structures) can be used to detect deviations in quality parameters and how Principle Component Analysis (PCA) can be used to determine abnormal conditions.
FOPDT Modeling of Process Response
Application of the latest sensor technologies enables cell characteristics as well as substrate and metabolic byproduct concentrations to be measured in a bioreactor.
Autoclaveable auto-samplers transform automated multifunctional analyzers into at-line instruments. In both at-line and online types, the sample periods are short relative to response times of a cell culture, sothese sensors open the door to closedloop concentration control.
Strategies for control of glucose concentration in perfusion or fed batch bioreactors have been proposed [1] but their implementation has been frustrated by the need for direct and reliable measurement. As far back as the 1980’s, it was suggested that glucose/glutamine ratio control would enhance cell growth, cell viability and product quantity in monoclonal antibody production. [2] The nature of the input and output relationships for new sensor-based control loops can most effectively be characterized by the identification of first order plus dead time (FOPDT) models.
Nonlinear input/output relationships can be characterized in a piecewise linear manner by breaking the control range into linear segments and identifying a unique FOPDT model in each segment. Turbidity as a measure of cell growth is an example of a fixed nonlinearity that can be segmented over the range of the measured variable or signal. FOPDT models of the process gain and dynamics may change over the range of a measured variable. Once this relationship is known, then the tuning of the control may be automatically changed to compensate for the nonlinearity.
Process Development with High Fidelity Models
High fidelity models used for design, control and optimization of cell culture bioreactors describe the relationship between substrate utilization, cell growth and product formation. They are first principle models from a chemical engineering view point because they are based on mass and energy balances and they describe compressible and incompressible phases.
The pH is computed from a charge balance equation. Since high fidelity models are parameterized differential equations and depend on experimental data, they are also considered semi-empirical. In most cases, high fidelity models can extrapolate better than purely empirical models and thus can be used to examine process operation over a wider range.
Cell culture high fidelity models must account for viable and non-viable cells and recombinant microbe models must describe biomass segregation so they can be considered structured models. High fidelity models have been created for recombinant bacteria, fungi, yeast and mammalian cell cultures.
All the models are broken into three phases; a bulk liquid phase, a sparge gas phase and an overhead or sweeping gas phase. On a distributed control system, a practitioner can assemble a high fidelity model from a library of simpler models implemented in composite blocks. A composite block is a container for parameters and other control blocks. At the bottom level of the bioreactor simulations, composite blocks have input and output parameters and calculation blocks. At higher levels in the simulation, composite blocks still contain input and output parameters and nested composite blocks.
Each of the gas and liquid phases in a bioreactor high fidelity model is represented by a higher level composite block. Unsteady state component, mass and energy balance calculations are contained in each block. The phases also contain mixing and mass transfer composite blocks. A single kinetics block contains growth and product formation blocks and substrate utilization blocks.
These blocks in turn contain at the lowest level composite blocks representing Michaels Mention saturation kinetics combined with inhibition. This block architecture allows for the creation of a library and the flexibility to represent bacterial, fungal and cell culture bioreactors. The fermenter or bioreactor composite block is combined in a module with other composite blocks representing mass and energy balances of valves, pumps and flow meters to create a virtual process. In other words, composite blocks from a library are interconnected to match a piping and instrument diagram of an actual bioreactor. If a control system configuration already exists, it can be copied and mapped to this plant simulation module to create a virtual plant.
If a control configuration does not exist, one can be created and tested in a virtual plant environment before the physical plant is completed. Batch recipes can be created and tested before clinical material is needed from pilot scale bioreactors. In a virtual environment, the process operation may be examined by running the process model and control faster than real time.
The fast execution allows users to play “what if” scenarios and design experiments that may reduce a process development batch schedule. [3] In production, the predictive capability of the virtual plant has the potential to infer unmeasured or unmeasureable process variables like product concentration. The accuracy of the inferential calculation can be maintained by adapting model parameters to changes in the actual plant.[4]
Data Analytics with Multivariate Statistical Models
Multivariate statistical models can monitor batch quality online, continuously. Monitoring can begin as early as the pilot scale clinical trial stage of product development. Alarm limits or univariate statistical techniques cannot be used to monitor quality since those techniques do not account for cross correlation and/or co-linearity present in cell culture or microbial batches.
Multivariate techniques for bioreactor quality monitoring and process control provide a solution by converting process variables that may be collinear and cross correlated to independent, uncorrelated variables called principal components. Based on principal component techniques, Squared Prediction Error (SPE), and Hotelling’s control charts can be developed to reflect overall batch operation.
Two types of multivariable analysis used online are Principal Component Analysis (PCA) and Partial Least Squares or Projection to Latent Structures (PLS). PCA monitors batch variables and states to verify the preservation of cross correlation and co-linearity upon which the model is based. PCA is most often used to detect process or measurement faults during a batch. PLS predicts output parameters based on input variables and the current process state. The output parameters may be the end of the batch or the endpoint product quality.
Both methods use empirical models based on a reference set of good batches. To be effective, these reference batches must capture the variability expected in the batch. Too little variation may lead to false alarms and too much variability can render the analysis insensitive. To build a model, the reference batches must be aligned so the data is synchronized at each point of the batch and all batches have common end points.
For example, a phase transition may wait for a tank to reach a predefined temperature. The time to reach that temperature and end the phase is not likely to be the same in any two batches. The method of synchronizing batches with the broadest application is Time Warping, [5], [6].
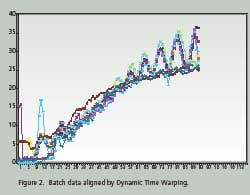
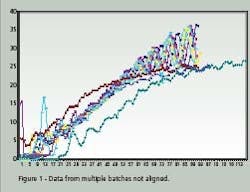
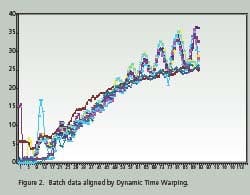
Time Warping is demonstrated as a feature match between two time series. The time series are non-linearly ‘warped” in the time dimension. The best results are obtained when a pattern or trajectory is optimized. Dynamic Programming is used to match elements of the time series so as to minimize discrepancies in each corresponding trajectory subject to constraints; hence the name Dynamic Time Warping. Constrains include sample beginning and end points, a monotonic solution and local continuity. Figures 1 and 2 compare batch data before and after alignment by Dynamic Time Warping.
Note how the oscillations are superimposed and the batch end points are equal after alignment. PCA and PLS techniques process continuous data in two dimensions; time and value. Batch data, on the other hand, is three dimensional; batch, value and time. Before PCA or PLS processing, batch data must be unfolded to two dimensions. There are several ways to unfold batch data.
Initially, batch-wise unfolding and variable-wise unfolding were considered separately. Batch-wise unfolding results in a two-dimensional matrix with each row containing all the data from a single batch. Variable-wise unfolding results in a two dimensional matrix segmented by time slices of the batch.
Each column of the variable-wise unfolded matrix contains all the values of a variable for all batches in that time segment. PCA and PLS analysis on batch-wise unfolded data can detect deviation from a desired operating trajectory. But in online application the data set is not complete until the end of the batch and prediction is necessary for batch-wise unfolding.
Online PCA and PLC analysis of variable-wise unfolded data does not require equal batch lengths or prediction of future values. However, nonlinear, time varying trajectories remain in the data matrix and calculated loadings contain correlations between variables. Lee, et al, [5], eliminated both the time dependency and need of prediction by mean centering and scaling batch-wise unfolded data and then re-arranging the data variable-wise.
Hybrid unfolding is used to generate the results shown in Figures 1 and 2. On line prediction of batch quality with PLS is achieved by partitioning the entire batch into equally spaced statistical scans. Since Dynamic Time Warping is used to match the measured data to the reference batches, they are labeled DTW scans. Each time the running batch completes a DTW scan, a PLS analysis is performed and the final product quality is predicted.
Summary
First order plus dead time, high fidelity and multivariate statistical models are valuable tools for batch operation improvement. First order plus dead time models can be identified automatically and high fidelity models can be generated from a library of composite block modules. Multivariate statistical analysis has been adapted to batch processes with dynamic time warping and hybrid unfolding. These online models can accelerate design of experiments and process design.
References
- Kleman G.L.,Chalmers J. J., Luli G W, Strohl W R, A Predictive and Feedback Control Algorithm Maintains a Constant Glucose Concentration in Fed-Batch Fermentations, APPLIED AND ENVIRONMENTAL MICROBIOLOGY, Apr. 1991, p. 910-917
- Luan Y T, Mutharasan R, Magee W E, Effect of various Glucose/ Glutamine Ratios on Hybridoma Growth, Viability and Monoclonal Antibody Formation, Biotechnology Letters Vol 9 No 8 535-538 (1987)
- McMillan G, Benton T, Zhang Y, Boudreau M, PAT Tools for Accelerated Process Development and Improvement, BioProcess International Supplement MARCH 2008.
- Boudreau M A, McMillan G K, New Directions in bioprocess Modeling and Control. ISA. Research Triangle Park, NC 2006.
- Lee J M, Yoo C K, Lee I B, Enhanced process monitoring of fedbatch penicillin cultivation using time-varying and multivariate statistical analysis. Journal of Biotechnology, 110 (2004) 119-136.
- Cinar A, Parulekar S J, Ündey C, Birol G, Batch Fermentation Modeling, Monitoring, and Control. Marcel Dekker, Inc. New York, NY 2003.
Authors
Corresponding author Michael Boudreau and Gregory McMillan are principal consultants for Emerson Process Management. Mr. Boudreau can be reached at [email protected]