ICH Guidances (Already) Show Their Age

Editor’s Note: This is the first of several articles that will review ICH guidelines.

The tools for a safe and well-produced pharmaceutical and nutraceutical supply in the country and world are in the news every day: PAT (Process Analytical Technologies), QbD Quality by Design), the ICH (International Conference on Harmonization of Technical Requirements for Registration of Pharmaceuticals for Human Use) Q-guidelines (8, 9, 10), and, of course, newer updates to cGMP (originally written in 1978, 30 years ago). There will be more said about the new regulations for nutraceuticals and the US FDA’s mandate to add them to their regulatory umbrella at a later date. For now, let’s just examine prescription pharmaceutical (and biopharmaceutical) production and analysis.

In the US, we have Guidances (PAT, for instance), while, for multi-national production and acceptance, the ICH is the lead organization. The unity of having major producers and consumers agree on guidelines for drug analysis (and purity and stability, etc.) is a boon to all parties. However, since these are well-thought out compromises, by nature they take time to formalize. Some date back well over a decade and pre-dated the QbD concept. This series will examine the various ICH guidelines and discuss their applicability to PAT/QbD as written.

The first to be examined is the ICH Guidance for the analysis (for release) of solid dosage forms: Guidance ICH Q2 (R1) [formerly Q2A/Q2B]. Any company following the suggested release criteria will allow a product to be accepted in all ICH signatory countries, avoiding an arcane mix of national test compliances.

In short, ICH Q2 (R1)’s main criteria are (1): 

Repeatability: A minimum of six readings of one sample at 100% of target concentration, or minimum of three readings on each of three samples with different concentrations of analyte.

Intermediate Precision: Measurement of the samples under variant conditions, using the same procedures for precision to determine the effect of random events, due to analysts, equipment, different days, etc.

Specificity: Definition of specificity as the ability to assess unequivocally the analyte in the presence of components that may be expected to be present, such as impurities, degradation products, and matrix components. Lack of specificity of an individual analytical procedure may be compensated by other supporting analytical procedures.

Accuracy: A minimum of three samples at each of three concentration levels. “Comparison of the results of the proposed analytical procedure with those of a second, well-characterized procedure, the accuracy of which is stated and defined.”

Range: 80% to 120% of target for assay; 70% to 130% of target for content uniformity.

Robustness: The sensitivity of the analytical procedure to extraneous variables that can be controlled, such as laboratory temperature and humidity.

Linearity: Computation of linear least-squares line through data; evaluation of regression statistics. Commonly accepted statistics include: slope, intercept, correlation coefficient (R or R²), standard error of estimate (SEE). Basically, are test results proportional to analyte concentration?

These are well-thought out guidelines, discussed fully by all ICH members (which also includes observers from regulatory agencies). However, it appears that the members only considered laboratory testing for final release. There is no mention of real-time, on-line results being generated or evaluated. And, based on most common practices, the concepts were actually based on standard QC laboratory analyses, almost exclusively using HPLC.

For PAT and QbD, there is a logic gap. If an analyst were to use, for example, near-infrared on intact tablets, he/she would quickly stumble over the ICH guidelines. Now, assuming we are performing a spectroscopic analysis of process samples (e.g., tablets), let us examine the appropriateness of the ICH guidelines. [The comments on ICH Q2 (R1) are based on NIR work performed on commercial tablet and capsule analyses as per FDA, USP, and ICH guidelines. The results were published in references 2 and 3.]

Range
Let’s start with the easiest to modify, range. The ranges of 80-120% for assay and 70-130% for content uniformity are quite decidedly based on HPLC methodology. In LC, the API (Active Pharmaceutical Ingredient) and excipients are weighed into a flask, an appropriate solvent is added, and the drug substance dissolved for analysis. The so-called “recovery” is, in fact not a recovery, since the dosage forms were not actually produced within the specified ±30% (of label claim) range. In most cases this range of products is physically impossible to produce (e.g., an aspirin tablet is >99% API; making a 130% tablet, at the specified weight, is not possible). In addition, making tablets so far OOR triggers a GMP recalibration of the equipment and method, even if deliberate.

In a whole-tablet spectroscopic assay, the samples need to be generated by the actual process. It has also been established that the “process signature,” a concept upon which much QbD work is based, will change as the synthetic tables are made, even if they are produced on the same equipment as the commercial product. The synthetic tablets may very well be far outside the “design space” of the method (but that topic is for another article).

Solution: a realistic working range that could expand as actual excursions in production are discovered. The range would be determined by actual fluctuations in the process. Should a value outside our working range happen, it may be added to out equation for future use (after being assayed by the compendial method). This could well mean a beginning range for a spectroscopic (Chemometric) equation being constructed on tablets from, for instance, 96 to 103% of label range in a well-regulated cGMP process. Unfortunately, this may impact the next topic discussed.

Linearity
The next, most problematic parameter is linearity. The common approach, usually based on a Beer’s law calibration, is to take the API and excipients, weigh the appropriate amount into volumetric flasks, add the appropriate solvent (s), extract, and fill to volume. The range is usually 50 to 150% of label claim. The resultant calibration curve is, in reality, weighed API in solution versus the resultant UV Absorbance.

This is only a manner in which to determine that the HPLC detector gives a predictable, linear response to the pure, separated API in solution. What is generated in a process method, using something such as NIR, is a comparison between HPLC results (only required to be ±1% between duplicate injections) and the predicted NIR values (reproducible to ±0.001%). The graph is not comparable to a simple concentration versus Absorbance plot. In any case, the LC vs. NIR results are plotted and a linear least squares best-fit line is calculated and the statistics evaluated for “linearity.”

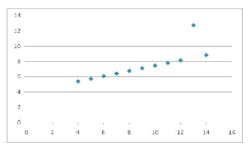
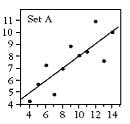
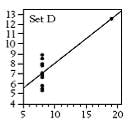
The standard measurements from this calibration line are R (correlation coefficient), slope, intercept, and standard error of estimate (SEE). Some work done years ago by a statistician named Frank Abscombe (4) showed that widely varying synthetic data sets (ranging from a somewhat linear set through a parabolic curve to other odd configurations) could all have the same statistics for the quantities mentioned above. As the graphed data is examine (see below), it becomes apparent that we may have been using the wrong statistics for linearity.

[These synthetic data are listed in Tables 1-4, and the resultant scatter plots are shown in Figures 1-4. While these plots show wildly different shapes, the intercepts, slopes, and correlation coefficients were identical, as seen on Table 5. These data would seem to cast “common practice” into a somewhat dubious light for process related analyses.]