• Magazine
  • ENEWS
  • SUBSCRIBE
  • WEBINARS
  • PODCASTS
  • EBOOKS
    1. Home

    A Framework for Technology Transfer to Satisfy the Requirements of the New Process Validation Guidance: Part 2

    May 22, 2012
    In the life of any drug product, the technology transfer of a process is a complex matter, made more complicated by the new definition of the Process Validation (PV) guidance issued by FDA in January 2011.
    1660254330784 Tech Fig1

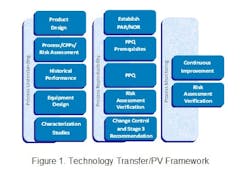
    In the life of any drug product, the technology transfer of a process is a complex matter, made more complicated by the new definition of the Process Validation (PV) guidance issued by FDA in January 2011. In Part 1 of this series we have attempted to lay out a practical approach to successful transfer citing a real life example. We discussed the activities required to identify and establish an effective Proven Acceptable Range (PAR) and Normal Operating Range (NOR) for a legacy product as defined by the technology transfer framework used for this project. The framework is based upon Pharmatech Associates’ Process Validation (PV) model shown below in Figure 1.

    tech_table1

    Part 2 will pick up where we left off in the framework and discuss the considerations in developing an effective sampling plan and acceptance criteria for the Stage 2 Process Performance Qualification (PPQ) and how to transition to the Stage 3 Continuous Monitoring phase of the new PV guidance. PPQ PrerequisitesWith the new PV guidance, the prerequisites for moving to PPQ are the same as the requirements defined in the original 1987 guidance. The expectation before moving forward to demonstrating process reproducibility includes completion of the following elements:

    • Facility and Utility qualification
    • Equipment qualification (IQ,OQ and PQ or equivalent) 
    • Analytical Method Validation is complete and Measurement System Analysis (MSA) has concluded that the resolution of the method is appropriate
    • Cleaning Validation protocol; Cleaning method development and validation 
    • Upstream processing validation such as Gamma irradiation of components if applicable, etc, are complete for the new batch size 
    • Environmental Monitoring program is in place for the new facility
    • Master Batch Record 
    • In-process testing equipment is qualified, MSA complete and acceptable, method validated and SOP in place

    In a technology transfer exercise these elements must be applied to the new equipment and include the larger commercial batch size consideration. If all the elements are not complete prior to beginning the PPQ runs then a strategy may be developed, with the participation of QA, to allow concurrent processing of the PPQ lot and process prerequisites. For example, if cleaning validation has not been completed prior to the PPQ runs, and the PPQ lots are intended for commercial release, then a risk-based approach to the cleaning validation may be adopted with studies conducted concurrently with the manufacture of the lots  with the caveat that the lots are not releasable until the cleaning validation program is complete. If such an approach is adopted then consideration must be given to both the major clean procedure, typically performed on equipment when changing products, and the minor clean procedure, typically performed during a product campaign.

    In our case study process, all prerequisites were complete with the exception of cleaning validation which was conducted concurrently. The new process site used a matrix approach to cleaning validation, bracketing its products based upon an assessment of the API/Formulation solubility, potency, LD50 and difficulty-to-clean profiles. For the purposes of the PPQ runs, only the major clean procedure was used between lots since the minor clean procedure had not been qualified.

    PPQ Lots
    To establish a PPQ plan that is efficient in demonstrating process reproducibility the considerations for sampling testing and establishing acceptance criteria must be thoughtfully considered, especially for products with limited development- or performance data.

    PPQ Objectives
    To cite the PV guidance, the objective of the Process Performance Qualification is to “confirm the process design and demonstrate that the commercial manufacturing process performs as expected.” The PPQ must “establish scientific evidence that the process is reproducible and will deliver quality products consistently.” We take key points from this objective in turn to establish acceptance criteria as in the following examples:

    • Process performs as expected: commercial performance is inferred from process knowledge gained during the Process Design stage;
    • Process is reproducible; process is under statistical control and is, therefore, predictable;
    • Process delivers quality products consistently: process is statistically capable of producing product that meets specifications (and in-process limits) and will continue to do so.
    The relationship between critical process parameters and quality attributes is defined through process knowledge. Therefore, when critical process parameters are controlled within their normal operating range (NOR), we should expect quality attributes to be statistically predictable and reproducible. It is clear that producing three commercial lots in a row to meet its specification limits is no longer sufficient to meet process qualification objectives. We must develop a statistical prediction for the acceptance criteria of quality attributes which is typically much more rigorous than simply meeting the specification limit.Considerations on SamplingSince the new PV guidance focuses on quality by design and control, there is greater interest in the identification and control of critical parameters to ensure that critical quality attributes throughout the lot are predictable. We cannot test the entire lot for the quality attributes, but we can control the parameters, and they should predict those quality attributes. Sampling and testing now become a verification of what we should already expect to occur. A sample from a lot does not tell us the value of a quality attribute since that quality attribute could be variable throughout the lot. In statistical terms, this is known as the population. However, statistics can help us infer (but never truly know) a likely range of a lot’s mean value for a quality attribute, expressed as a confidence interval. We could also calculate a similar confidence interval for the standard deviation of the lot.The mean of the sample values is not as important as the calculated confidence interval (usually chosen as 95 percent confidence) for the lot’s mean. This is because it is the limit of the confidence interval that must meet our acceptance criteria, since we want to be able to infer that the true mean—and the true standard deviation—meets the acceptance criteria, not just individual tested samples.Determine PPQ Acceptance CriteriaTo determine the acceptance criteria for PPQ lots, we use the process knowledge from the process design to make an estimate of the process mean—in other words, where the process centers—and the process standard deviation—or how the process varies around the center—for each critical quality attribute. This allows for a statistical comparison of the PPQ lots’ means to the expected process mean. The comparison between two means is done using the “t-Test,” to evaluate any difference in two independent samples. The acceptance criteria is successful when the t-Test concludes that the difference between the lot’s population mean and the predicted process mean is less than the largest predicted variation of the predicted process mean, calculated from the process standard deviation. In statistical terms, this describes the alternative hypothesis (H1) of the t-Test:    H1: μ1 – μ2 < (Target Difference)Where, μ1 and μ2 are the predicted process mean and the population mean of the PPQ lot and the Target Difference is the predicted variation in the process mean. For the t-test, when the null hypothesis (H0) is not significant, the alternative hypothesis (H1) is concluded to be true.There are several methods of predicting the process mean and its variation from process design data:1)    Use a predictive model: When DOEs are used during process design and a strong relationship (correlation and mechanism) is shown between critical process parameters and critical quality attributes, a mathematical model can be used to predict how variation in the process parameter affects the quality attribute. It is assumed that the PAR of the process parameter is such that the quality attribute will be within specification. Variation in the model itself must be considered since the model equation usually predicts the quality attribute on average rather than for individual PPQ lots, which will vary from the average. Alternatively, scale-up models are also useful at predicting process shifts from pilot to commercial scale. 2)    Analyze Historical Performance: When performing a technical transfer from one commercial site to a new commercial site, the historical process mean and its variation can be calculated to predict performance at the new site.3)    Analyze Development Performance: Development lots produced during Process Design are used to determine the PAR for critical parameters. Consequently, these extreme set point runs will produce critical quality attributes at their highest deviation from the process mean. Variation in the raw materials lot (and any critical material attributes) must be considered in the predicted process variation. A limited number of development lots may not have experienced the full variation due to the limited number of raw material lots used. As mentioned before, the t-Test is a statistical comparison of means. To compare standard deviations between lots the statistical test is the F-test (for normally distributed data) or Levene’s test (no assumption of normal distribution). The acceptance criteria for the standard deviation of a quality attribute (variation between samples in a lot) must consider how the attribute varies from lot to lot in addition to the variation within each lot to ensure all portions of the lot have a high likelihood of meeting specification.Determine the Number of Samples RequiredCertain sampling plans commonly used during PPQ are predefined in various guidance and standards. One example is blend uniformity in which both the minimum sampling requirements and the acceptance criteria are defined. Another is Bergum’s Method for Content Uniformity. For user-defined plans (e.g., t-Test) the minimum number of samples must be calculated to ensure that a valid statistical conclusion may be drawn.For the t-Test, F-test, or Levene test the number of samples is calculated using a power calculation for the specific test. The power calculation uses the conceptions of alpha risk (Type I error, the risk of failing a criteria which actually passes) and beta risk (Type II error, the risk of passing a criteria which actually fails). Power is 1– beta is targeted at either 0.8 (20 percent beta risk) or 0.9 (10 percent beta risk); the actual risk of the sampling plan is determined after the number of samples is known. Calculating the sample size using a power calculation will require the significance level (alpha risk), the estimated maximum standard deviation (between samples), and a target difference. Figure 1 is an example power curve showing the number of samples for different target power (0.8 and 0.9) with a standard deviation of 1. From this chart, the sample size is determined by the first curve above the target power for a given target difference. Our choice of target difference is determined by the acceptance criteria of the t-Test. That is, the largest variation predicted in the process mean.

    tech_fig1
    Figure 1. Sample Size by Power Curve for T-testLot Acceptance Sampling PlansWhen sampling for attributes that are discrete (pass/fail) rather than continuous (a numeric value), the sampling plan is determined by an operating characteristic curve instead of a power curve. Frequently used for visual defects, these plans are either calculated or selected from the ANSI Z1.4-2008 standard for sampling by attributes. In our case, the manufacturer’s quality assurance group chose the Acceptance Quality Level (AQL) for the attribute, because it represented the maximum process average of defects for that attribute over time. The desire for PPQ lots is to increase the number of samples (i.e. discrimination of the sample plan). However, shifting the AQL is not recommended since the AQL is not representative for individual lots in isolation. To create a more discriminating sampling plan for PPQ, the Limiting Quality (LQ, also called Lot Tolerance Percent Defective, LTPD) is the preferred method for creating a more discriminating plan for PPQ. Figure 2 compares a standard lot plan under Z1.4 (General Inspection Level II) to a more discriminating PPQ lot plan (General Inspection Level III). The number of samples increases from 500 to 800 and the LQ at 10 percent acceptance changes from approximately 0.77 percent defective to 0.65 percent defective. These types of sampling plans are only suitable for individual lot acceptance; they do not determine the actual percent defective for a lot. These plans only assure that lots above the LQ have a low (10 percent or less) probability of being accepted under this plan.
    tech_2

    Figure 2. Limiting Quality Comparison between Z1.4 Sample PlansNumber of PPQ LotsThe PV Guidance no longer defines the number of lots required for PPQ; it is left to individual manufacturers to justify how many lots are sufficient. There is no safe harbor for producing three PPQ lots since justification must be made for any number of lots. In order to make any reasonable argument of reproducibility, it would be expected that the minimum number of lots be no less than two to three.

    It is usually not necessary to operate process parameters at the extremes of the NOR since this should have been previously established. As such, the set points of process parameters are not changed between PPQ lots and do not impact the number of PPQ lots required. In determining the number of lots consideration should be given to understanding the source and impact of variation on quality attributes. Suggested sources of variation to consider are:

    • Number of raw material lots. In particular, when a critical material attribute is identified;
    • Number of commercial scale lots previously produced during Process Design;
    • Number of equipment trains intended for use with commercial production;
    • Complexity of process and number of intermediate process steps;
    • History of performance of commercial scale equipment on similar products;
    • Number of drug strengths;
    • Variation of lot size within commercial equipment;
    • In-process hold times between process steps;
    • Number of intermediate lots and mixing for downstream processes.

    It is recommended to perform a risk analysis of these sources of variability. The number of PPQ lots can then be determined by matrix design of the sources with the highest risk to variation of quality attributes. Those sources of variability, which cannot be included in the PPQ, should be considered for monitoring during Stage 3 - Continuous Process Verification.

    After completing the PPQ analysis, the team revisited the risk matrix to reflect the commercial operation.  This data was included in the Stage 2 final report. 

    Stage 3: Process Monitoring
    The last stage of the new PV lifecycle is process monitoring. While monitoring has been part of the normal drug quality management system (QMS), the new PV guidance advocates moving beyond the normal CQAs reported in a product’s Annual Product Review (APR) and extending them to include the CPPs that have been identified as critical to process stability.

    For the product in question, a protocol was drafted to gather data over the next 20 lots to establish alert- and action limits relating to process variability. This data was intended to be reported as part of the product scorecard and included in the APR. One key consideration or expectation of Stage 3 of the PV model put forth in the guidance is the ability to make adjustments to the process without having to revalidate the process. The underlying premise behind this assumption is that there is sufficient process understanding from Stages 1 and 2 to predict the impact of the change on product performance. Updating the risk model as new and greater understanding becomes available will allow the previous understanding to be considered when contemplating a process adjustment in the future.

    Conclusion
    Transferring a legacy process that has limited development and characterization data requires a clear data gathering and analysis strategy to be able to meet the requirements of the new PV guidance. The prerequisites to PPQ that would be routine as part of a new drug development exercise must be considered before moving the product to the new process train to ensure the key expectations of the quality management system are addressed for any potential commercial material manufactured as part of the PPQ runs.

    There is no single solution to establish the final PPQ design, sampling and acceptance criteria. The framework applied for this technology transfer process provided a practical methodology for considering the key elements required to control the sources of variability that can affect process reproducibility commercially while meeting the primary elements of the new process validation guidance.

    General References
    1.    Guidance for Industry-Process Validation: General Principles and Practices, January 2010, Rev. 1.
    2.    ANSI/ASQ Z1.4-2008, "Sampling Procedures and Tables for Inspection by Attributes."
    3.    Kenneth Stephens, The Handbook of Applied Acceptance Sampling Plans, Procedures and Principles, ISBN 0-87389-475-8, ASQ, 2001.
    4.    G.E.P Box, W.G. Hunter, and J.S. Hunter, Statistics for Experimenters, ISBN 0-471-09315-7, Wiley Interscience Series, 1978.
    5.    Douglas C. Montgomery, Design and Analysis of Experiments, 5th Ed., ISBN 0-471-31649-0, Wiley & Sons, 2001.
    6.    Schmidt & Launsby, Understanding Industrial Designed Experiments, 4th Ed., ISBN 1-880156-03-2, Air Academy Press, Colorado Springs, CO, 2000.
    7.    Donald Wheeler, Understanding Variation: The Key to Managing Chaos, ISBN 0-945320-35-3, SPC Press, Knoxville, TN.
    8.    W.G. Cochran and G.M. Cox, Experimental Designs, ISBN0-471-16203-5, Wiley and Sons, 1957.
    9.    Box, G.E.P., Evolutionary Operation: A method for increasing industrial productivity, Applied Statistics 6 (1957) 81-101.
    10.    Box, G.E.P. and Draper, N.R., Evolutionary Operation: A Statistical Method for Process Improvement, ISBN 0-471-25551-3, Wiley and Sons, 1969.
    11.    Pramote Cholayudth, Use of the Bergum Method and MS Excel to Determine
    The Probability of Passing the USP Content Uniformity Test, Pharmaceutical Technology, September 2004.

    About the Author

    Bikash Chatterjee and Mark Mitchell | Pharmatech Associates